PARABOLA
| SECCIONES CÓNICAS |
| Una sección cónica, es la curva de intersección de un plano con un cono circular recto. Existen tres tipos de curvas que se obtienen de esta manera: La parábola, la elipse incluyendo la circunferencia como un caso especial) y la hipérbola. (Ver fig. 6.1.) |
| 6.1 LA PARABÓLA | ||
| Definiciones i. Sea DD una recta dada del plano y F un punto del plano que no está en la recta dada. Se define la parábola como el lugar geométrico de los puntos P del plano cuya distancia al punto F es igual a la distancia a larecta DD. ii. La recta dada DD se llama DIRECTRIZ y el punto F se llama FOCO (fig. 6.1.1.) Frecuentemente se hace referencia a la parábola de directriz DD y de foco F y se denota por PDD-F. Esto es: | ||
Observaciones:
ii. Sea V el punto medio del segmento . Como ,
Como , entonces el punto V pertenece a la parábola. V es llamado VERTICE de la parábola.
entonces el punto V pertenece a la parábola. V es llamado VERTICE de la parábola.
 Como ,
Como , entonces el punto V pertenece a la parábola. V es llamado VERTICE de la parábola.
entonces el punto V pertenece a la parábola. V es llamado VERTICE de la parábola. El lugar correspondiente a la parábola es simétrico respecto a la recta . En efecto, si P’ es el simétrico de P respecto a la recta
En efecto, si P’ es el simétrico de P respecto a la recta , entonces PP’’ = P’’P’. Por lo tanto, el triángulo PP’’F es congruente al triángulo P’P’’F. De donde P’F = PF y como P’D’ = PD, entonces,
, entonces PP’’ = P’’P’. Por lo tanto, el triángulo PP’’F es congruente al triángulo P’P’’F. De donde P’F = PF y como P’D’ = PD, entonces, , lo cual nos muestra que P’ e PDD-F.
, lo cual nos muestra que P’ e PDD-F.
 En efecto, si P’ es el simétrico de P respecto a la recta
En efecto, si P’ es el simétrico de P respecto a la recta , entonces PP’’ = P’’P’. Por lo tanto, el triángulo PP’’F es congruente al triángulo P’P’’F. De donde P’F = PF y como P’D’ = PD, entonces,
, entonces PP’’ = P’’P’. Por lo tanto, el triángulo PP’’F es congruente al triángulo P’P’’F. De donde P’F = PF y como P’D’ = PD, entonces, , lo cual nos muestra que P’ e PDD-F.
, lo cual nos muestra que P’ e PDD-F. Ecuaciones Analíticas de la Parábola
En esta sección sólo se considerarán parábolas con el vértice V en el origen de coordenadas y cuyos focos estarán localizados sobre los ejes x ó y
Elevando al cuadrado ambos miembros de la última igualdad, y desarrollando los binomios, se obtiene: , y simplificando queda finalmente,
, y simplificando queda finalmente,
 , y simplificando queda finalmente,
, y simplificando queda finalmente, Recíprocamente, sea P(x, y) un punto del plano, cuyas coordenadas (x, y) satisfacen (1) y pruebe que P e PDD-F.

De esta forma se ha demostrado la parte i del siguiente teorema.
TEOREMA 1 (Ecuaciones de la Parábola)
i. La ecuación de la parábola que tiene su foco en F(p/2, 0) y por directriz la recta x = -p/2 (fig. 6.1.4) viene dada por : y2=2px(3). Recíprocamene si un punto P del plano, satisface (3) entonces P x PDD-F
ii. La ecuación de la parábola que tiene su foco en F(0, p/2) y por directriz la recta y = -p/2 (fig. 6.1.3.) es: x2 = 2py (4)
iii. Recíprocamente, si un punto P del plano, satisface (4) entonces P x PDD-F
Observaciones:
i. En la fig. 6.1.3. aparecen las gráficas de dos parábolas abiertas hacia arriba (en el caso de p>0) y hacia abajo (p<0), respectivamente y cuyos focos están localizados en el punto
F(0, p/2) y cuya directriz es la recta de ecuación y = -p/2.
F(0, p/2) y cuya directriz es la recta de ecuación y = -p/2.
Además, todos sus puntos son simétricos con respecto al eje y: de aquí que las ecuaciones que representan sus lugares geométricos, presentan únicamente a la variable x elevada en una potencia par.
ii. Igualmente, las gráficas de la fig. 6.1.4. corresponden a las gráficas de parábolas abiertas hacia la derecha (p > 0) e izquierda (p < 0) respectivamente, con focos en el punto F(p/2, 0) y cuya directriz es la recta de ecuación x = -p/2. Además todos sus puntos son simétricos con respecto al eje x, de aquí que las ecuaciones que representan sus lugares geométricos, poseen únicamente a la variable y elevada a su potencia par.
6.1.2. Traslación de Ejes
En el ejemplo 5 de la sección 5.6., se determinó que la ecuación de la circunferencia con centro en C(4,3) y radio 5 era:  ó
ó 
 ó
ó 
De lo anterior se concluye que a veces puede cambiar la ecuación sin cambiar la forma de la gráfica
Si en el plano cartesiano x - y se eligen nuevos ejes coordenados paralelos a los ejes x e y, se dice entonces que ha habido una "TRASLACIÓN DE EJES". Al fin de analizar los cambios que se presenten en las coordenadas de los puntos del plano al introducir un nuevo sistema de coorde- nadas x’ e y’ paralelo a los ejes x e y, se toma un punto fijo o’(h, k) que se llama: ORIGEN del nuevo sistema.
Sea ahora, un punto P(x, y) del plano, cuyas coordenadas están referidas al sistema con origen O(O, O) Entonces las coordenadas de P(x’, y’) referidas al sistema x’-y’ vienen dadas por las relaciones:
| x = x’ + h (1) y = y’ + k (2) llamadas: ECUACIONES DE TRASLACIÓN DE EJES, y que pueden deducirse fácilmente de la . |
Observación:
La traslación de ejes modifica la ecuación de una curva y algunas veces la simplifica, pero no altera la forma de la curva.
Una aplicación útil de la traslación de ejes se consigue cuando se obtienen las ecua- ciones generales de la parábola, con vértice en el punto V (h, k) referido al sistema x-y y para las cuales la directriz es perpendicular a uno de los ejes.
Si se toma como referencia los ejes x’ e y’, hallar las ecuaciones de la parábola con vértice en V(h, k), equivale a encontrar las ecuaciones de la parábola con vértice en (0, 0) referido al nuevo sistema.
Las ecuaciones  ,
, permiten escribir las ecuaciones en forma general de la parábola, como lo afirma el siguiente teorema:
permiten escribir las ecuaciones en forma general de la parábola, como lo afirma el siguiente teorema:
 ,
, permiten escribir las ecuaciones en forma general de la parábola, como lo afirma el siguiente teorema:
permiten escribir las ecuaciones en forma general de la parábola, como lo afirma el siguiente teorema: Teorema2 (Ecuaciones de la parábola. Forma general)
i. La ecuación de la parábola con vértice en el punto V (h, k), que tiene su foco en y por directriz la recta:
y por directriz la recta:

(fig. 6.1.7.) viene dada por:
(1)
 y por directriz la recta:
y por directriz la recta: 
(fig. 6.1.7.) viene dada por:

(1)
fig. 6.1.7.
ii. La ecuación de la parábola con vértice en el punto V (h, k), que tiene su foco en y por directriz la recta:
el punto V (h, k), que tiene su foco en y por directriz la recta: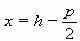
(fig. 6.1.8.) viene dada por:
(2)
ii. La ecuación de la parábola con vértice en
 el punto V (h, k), que tiene su foco en y por directriz la recta:
el punto V (h, k), que tiene su foco en y por directriz la recta: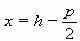
(fig. 6.1.8.) viene dada por:

(2)
"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""
____________________________________________________
Demostración: Es similar a la del teorema 1, aplicado al sistema x’-y’ y luego hacer e
e 
Observación: Las ecuaciones (1) y (2) del teorema 2, después de simplificarlas, pueden expresarse en la forma:
(3) 
(4)
En las ecuaciones (3) y (4) puede notarse que una de las variables aparece al cua- drado y la otra lineal. La parábola siempre se abre en la dirección del eje cuya varia- ble aparece lineal.
Así por ejemplo, la ecuación (3) representa una parábola que se abre hacia el semieje y positivo (si p > 0) o hacia el semieje y negativo (si p < 0). Igualmente, la ecuación (4) representa una parábola abierta hacia la derecha (si p > 0) o hacia la izquierda (si p < 0).
6.1.4. Valores máximos y mínimos de una parábola
Se ha visto en la sección precedente que la ecuación (1) puede escribirse (completando cuadrados) en la forma
(1) puede escribirse (completando cuadrados) en la forma (2) y representa una parábola cuyo eje focal es vertical, abierta hacia arriba (p > 0) ó hacia abajo (p < 0).
(2) y representa una parábola cuyo eje focal es vertical, abierta hacia arriba (p > 0) ó hacia abajo (p < 0).
Cuando la ecuación aparece en la forma (1), el signo de a (coeficiente de x2), determina si la parábola se abre hacia arriba o hacia abajo y también determina si el vértice es un punto máximo o mínimo de la curva.

(4)

En las ecuaciones (3) y (4) puede notarse que una de las variables aparece al cua- drado y la otra lineal. La parábola siempre se abre en la dirección del eje cuya varia- ble aparece lineal.
Así por ejemplo, la ecuación (3) representa una parábola que se abre hacia el semieje y positivo (si p > 0) o hacia el semieje y negativo (si p < 0). Igualmente, la ecuación (4) representa una parábola abierta hacia la derecha (si p > 0) o hacia la izquierda (si p < 0).
6.1.4. Valores máximos y mínimos de una parábola
Se ha visto en la sección precedente que la ecuación
 (1) puede escribirse (completando cuadrados) en la forma
(1) puede escribirse (completando cuadrados) en la forma (2) y representa una parábola cuyo eje focal es vertical, abierta hacia arriba (p > 0) ó hacia abajo (p < 0).
(2) y representa una parábola cuyo eje focal es vertical, abierta hacia arriba (p > 0) ó hacia abajo (p < 0). Cuando la ecuación aparece en la forma (1), el signo de a (coeficiente de x2), determina si la parábola se abre hacia arriba o hacia abajo y también determina si el vértice es un punto máximo o mínimo de la curva.
fig. 6.1.9. (a) fig. 6.1.9. (b)
Si como en la fig. 6.1.9.(a), la parábola se abre hacia abajo, el vértice V (punto mas alto de la curva) es llamado el punto máximo de la parábola. El valor de la ordenada correspondiente es el valor máximo de la función que ella representa.
Similarmente, si la parábola se abre hacia arriba (fig. 6.1.9.(b)), el vértice V es llama- do el punto mínimo de la parábola; y el correspondiente valor de y, es el valor mínimo de la función.
Toda función cuadrática, tiene un valor máximo o un valor mínimo, pero no ambos.
Si como en la fig. 6.1.9.(a), la parábola se abre hacia abajo, el vértice V (punto mas alto de la curva) es llamado el punto máximo de la parábola. El valor de la ordenada correspondiente es el valor máximo de la función que ella representa.
Similarmente, si la parábola se abre hacia arriba (fig. 6.1.9.(b)), el vértice V es llama- do el punto mínimo de la parábola; y el correspondiente valor de y, es el valor mínimo de la función.
Toda función cuadrática, tiene un valor máximo o un valor mínimo, pero no ambos.
*******************************************************
Hipérbola
Las asíntotas de la hipérbola se muestran como líneas discontinuas azules que se cortan en el centro de la hipérbola (curvas rojas), C. Los dos puntos focales se denominan F1 y F2, la línea negra que los une es el eje transversal. La delgada línea perpendicular en negro que pasa por el centro es el eje conjugado. Las dos líneas gruesas en negro paralelas al eje conjugado (por lo tanto, perpendicular al eje transversal) son las dos directrices, D1 y D2. La excentricidad e (e>1), es igual al cociente entre las distancias (en verde) desde un punto P de la hipérbola a uno de los focos y su correspondiente directriz. Los dos vértices se encuentran en el eje transversal a una distancia ±a con respecto al centro.Una hipérbola (del griego ὑπερβολή) es una sección cónica, una curva abierta de dos ramas obtenida al cortar un cono recto por un plano oblicuo al eje de simetría con ángulo menor que el de la generatriz respecto del eje de revolución.1
| Una hipérbola es el lugar geométrico de los puntos de un plano tales que el valor absoluto de la diferencia de sus distancias a dos puntos fijos, llamados focos, es igual a la distancia entre los vértices, la cual es una constante positiva. |
hipérbola
Debido a la inclinación del corte, el plano de la hipérbola interseca ambas ramas del cono.
Según la tradición, las secciones cónicas fueron descubiertas por Menecmo, en su estudio del problema de la duplicación del cubo,2 donde demuestra la existencia de una solución mediante el corte de una parábola con una hipérbola, lo cual es confirmado posteriormente por Proclo y Eratóstenes.3
Sin embargo, el primero en usar el término hipérbola fue Apolonio de Perge en su tratado Cónicas,4 considerada obra cumbre sobre el tema de las matemáticas griegas, y donde se desarrolla el estudio de las tangentes a secciones cónicas.
Según la tradición, las secciones cónicas fueron descubiertas por Menecmo, en su estudio del problema de la duplicación del cubo,2 donde demuestra la existencia de una solución mediante el corte de una parábola con una hipérbola, lo cual es confirmado posteriormente por Proclo y Eratóstenes.3
Sin embargo, el primero en usar el término hipérbola fue Apolonio de Perge en su tratado Cónicas,4 considerada obra cumbre sobre el tema de las matemáticas griegas, y donde se desarrolla el estudio de las tangentes a secciones cónicas.



















No hay comentarios:
Publicar un comentario